
Solved Consider the following functions. f(x) = x / x + 5,
f'(x) = u'(x) + v'(x) Now, differentiating the given function, we get; f'(x) = d/dx(x + x 3) f'(x) = d/dx(x) + d/dx(x 3) f'(x) = 1 + 3x 2. Example 2: Find the derivative of the function f(x) = 6x 2 - 4x. Solution: Given function is: f(x) = 6x 2 - 4x. This is of the form f(x) = u(x) - v(x) So by applying the difference rule of.
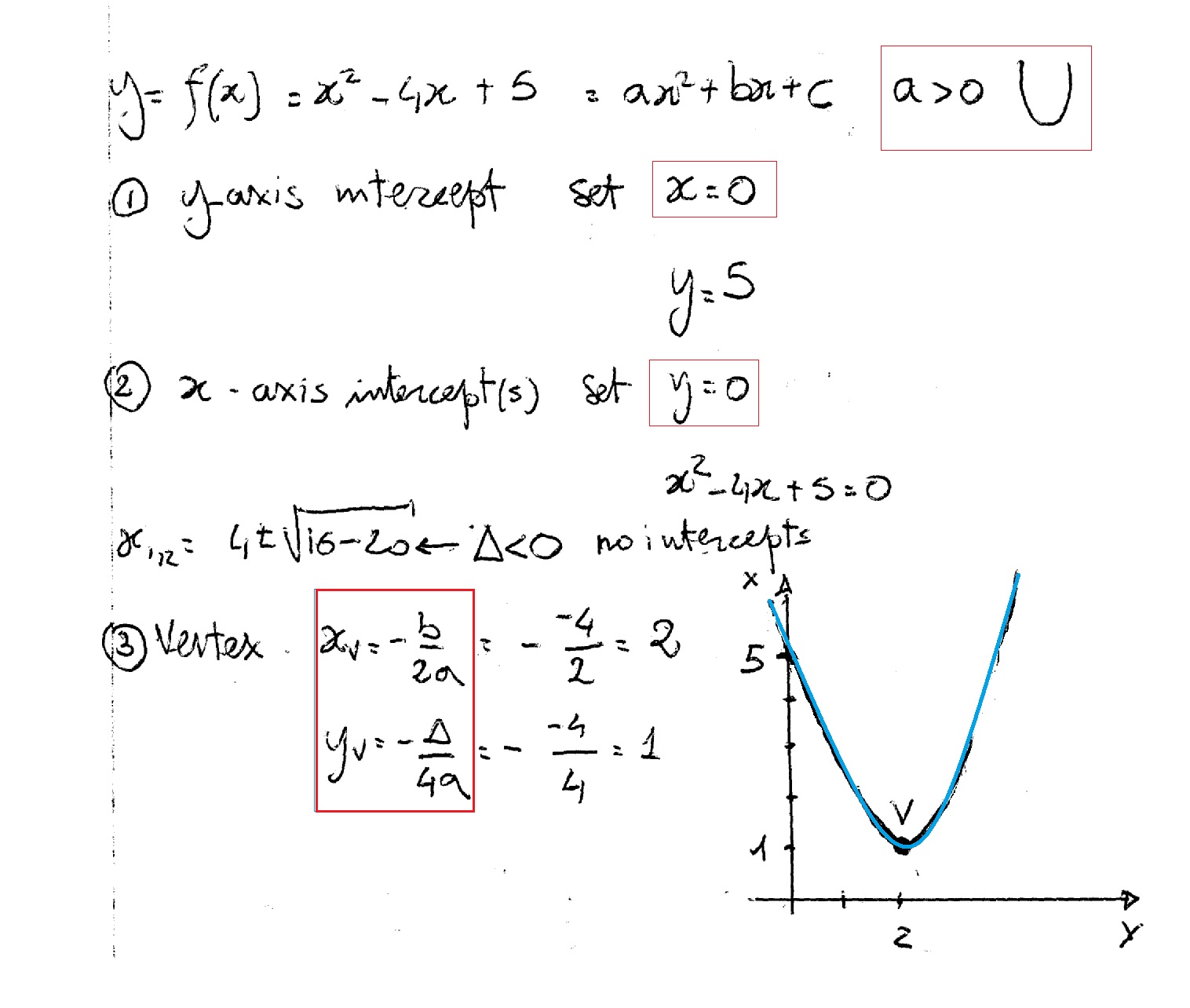
How do you graph f(x) = x^24x + 5? Socratic
This pattern works with functions of more than two variables as well, as we see later in this section. Example 14.5.1: Using the Chain Rule. Calculate dz / dt for each of the following functions: z = f(x, y) = 4x2 + 3y2, x = x(t) = sint, y = y(t) = cost. z = f(x, y) = √x2 − y2, x = x(t) = e2t, y = y(t) = e − t.

f(x) ☆ F(x) Wallpaper (35120236) Fanpop
We say "f of x equals x squared" what goes into the function is put inside parentheses () after the name of the function: So f (x) shows us the function is called " f ", and " x " goes in And we usually see what a function does with the input: f (x) = x2 shows us that function " f " takes " x " and squares it. Example: with f (x) = x2:
Graph of f(x), f'(x), and f''(x) (Calculus)
The Derivative tells us the slope of a function at any point. There are rules we can follow to find many derivatives. For example: The slope of a constant value (like 3) is always 0 The slope of a line like 2x is 2, or 3x is 3 etc and so on. Here are useful rules to help you work out the derivatives of many functions (with examples below ).
SOLUTION what is a domain of f(x)=52x
Roman numerals to numbers conversion calculator and how to convert.

Ex 13.1, 27 Find lim x>5 f(x), where f(x) = x 5 Ex 13.1
1. Yes. In mathematics it is more common to use a single letter (sometimes a Greek letter), but a function name can be anything. After all it's just a way to communicate to other humans what you're talking about, changing a name doesn't change the math. 2. Yes. A simple example is f (x,y) = x * y. 3. Yes.
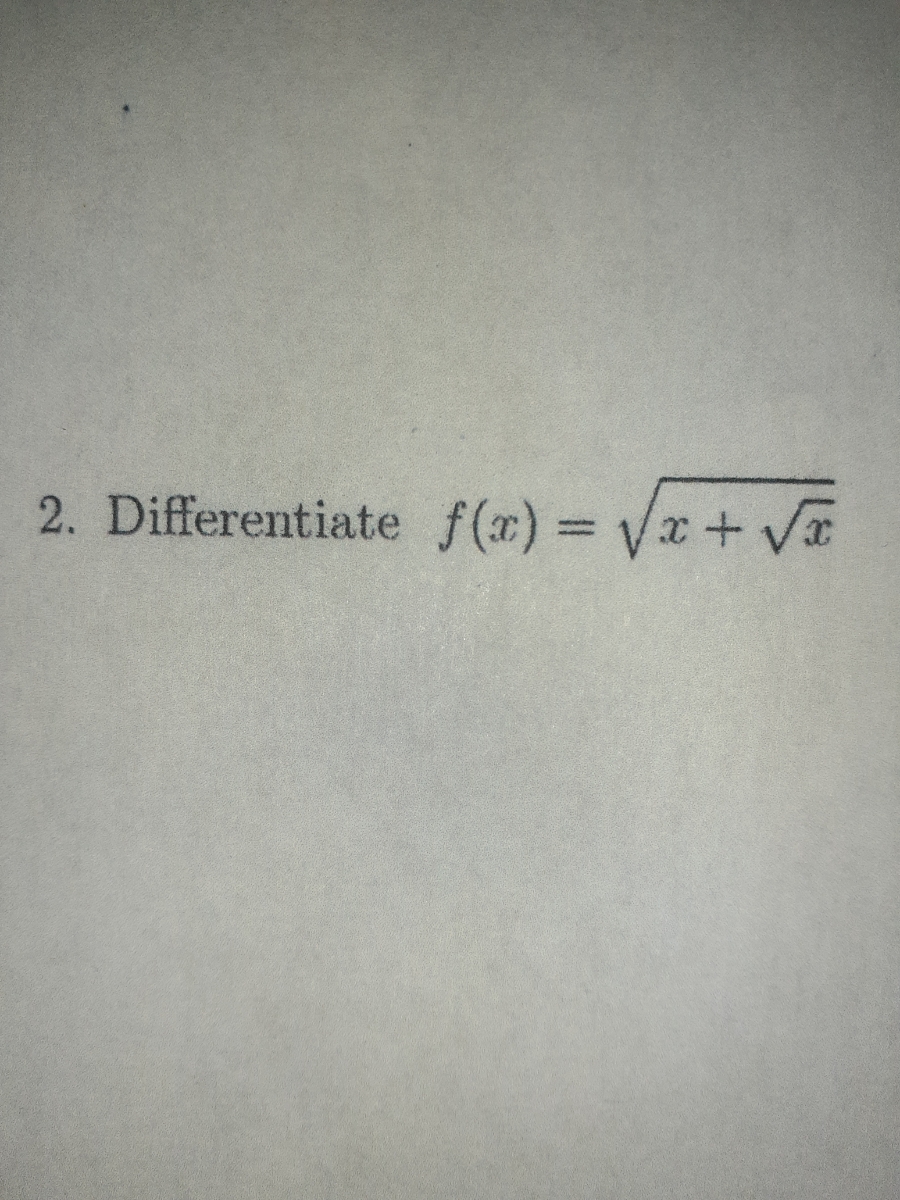
Answered Differentiate f (x) = V x+ V 3D bartleby
What is f(x)? It is a different way of writing "y" in equations, but it's much more useful!

Integral of f '(x)/f(x) Very Common Integral Calculus YouTube
Using implicit differentiation Using chain rule Quotient Rule Formula Proof Using Derivative and Limit Properties To prove quotient rule formula using the definition of derivative or limits, let the function f (x) = u (x)/v (x). ⇒ f' (x) = lim h → 0 [f (x + h) - f (x)]/h = lim h → 0 u ( x + h) v ( x + h) − u ( x) v ( x) h

Given the graph of the function `y=f(x)`, draw the graph of `y ="sgn"(x
The SEC v Ripple case saw an increase in activity on Thursday as the SEC and Ripple progress through remedies-related discovery. On Thursday, XRP gained 0.18%. Following a 6.03% rally on Wednesday.

What is the range of the function f (x) = (x + 5) (x + 1)
Here is Great Educational Songs & Animations for kids, toddlers, children, babies and EVERYONE!Learn English Alphabet, Phonics with words.Please enjoy watchi.

Composite Function Example 3 SPM Additional Mathematics
Integration by parts is a method to find integrals of products: ∫ u ( x) v ′ ( x) d x = u ( x) v ( x) − ∫ u ′ ( x) v ( x) d x. or more compactly: ∫ u d v = u v − ∫ v d u. We can use this method, which can be considered as the "reverse product rule ," by considering one of the two factors as the derivative of another function.
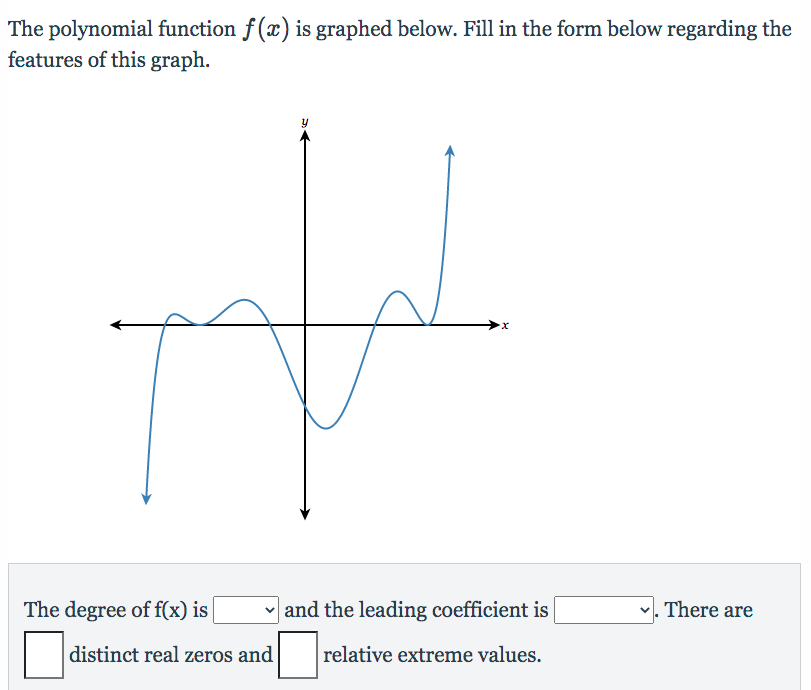
Answered The polynomial function f (x) is… bartleby
A function, by definition, can only have one output value for any input value. So this is one of the few times your Dad may be incorrect. A circle can be defined by an equation, but the equation is not a function. But a circle can be graphed by two functions on the same graph. y=√ (r²-x²) and y=-√ (r²-x²)

The function, "f" is defined by the following rule. f(x)=x5 Complete
Jan 21, 2014 at 15:57 Add a comment 2 Answers Sorted by: 14 The graph of $f (-x)$ is the mirror image of the graph of $f (x)$ with respect to the vertical axis. The graph of $-f (x)$ is the mirror image of the graph of $f (x)$ with respect to the horizontal axis. A function is called even if $f (x)=f (-x)$ for all $x$ (For example, $\cos (x)$).
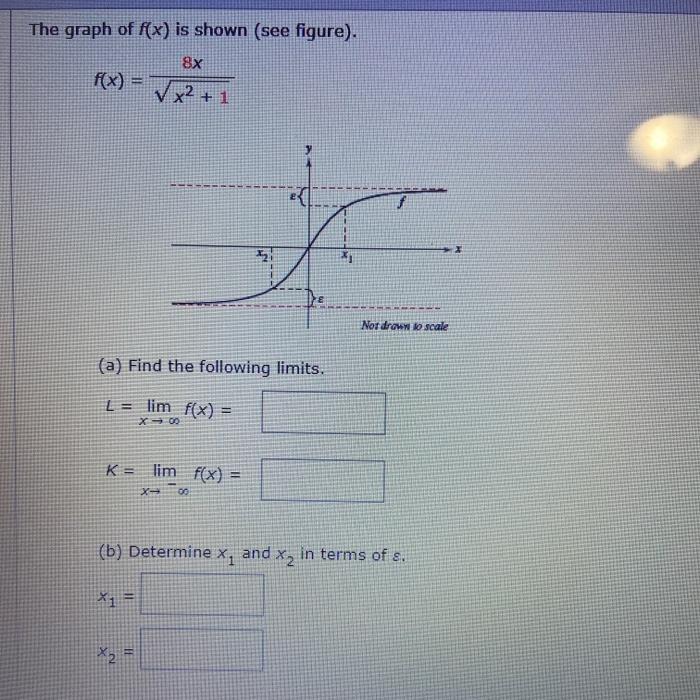
Solved The graph of f(x) is shown (see figure). 8x f(x) = V
lf c is any real number and if f(x) = c for all x, then f ' (x) = 0 for all x . That is, the derivative of a constant function is the zero function. It is easy to see this geometrically. Referring to Figure 1, we see that the graph of the constant function f(x) = c is a horizontal line. Since a horizontal line has slope 0, and the line is its.
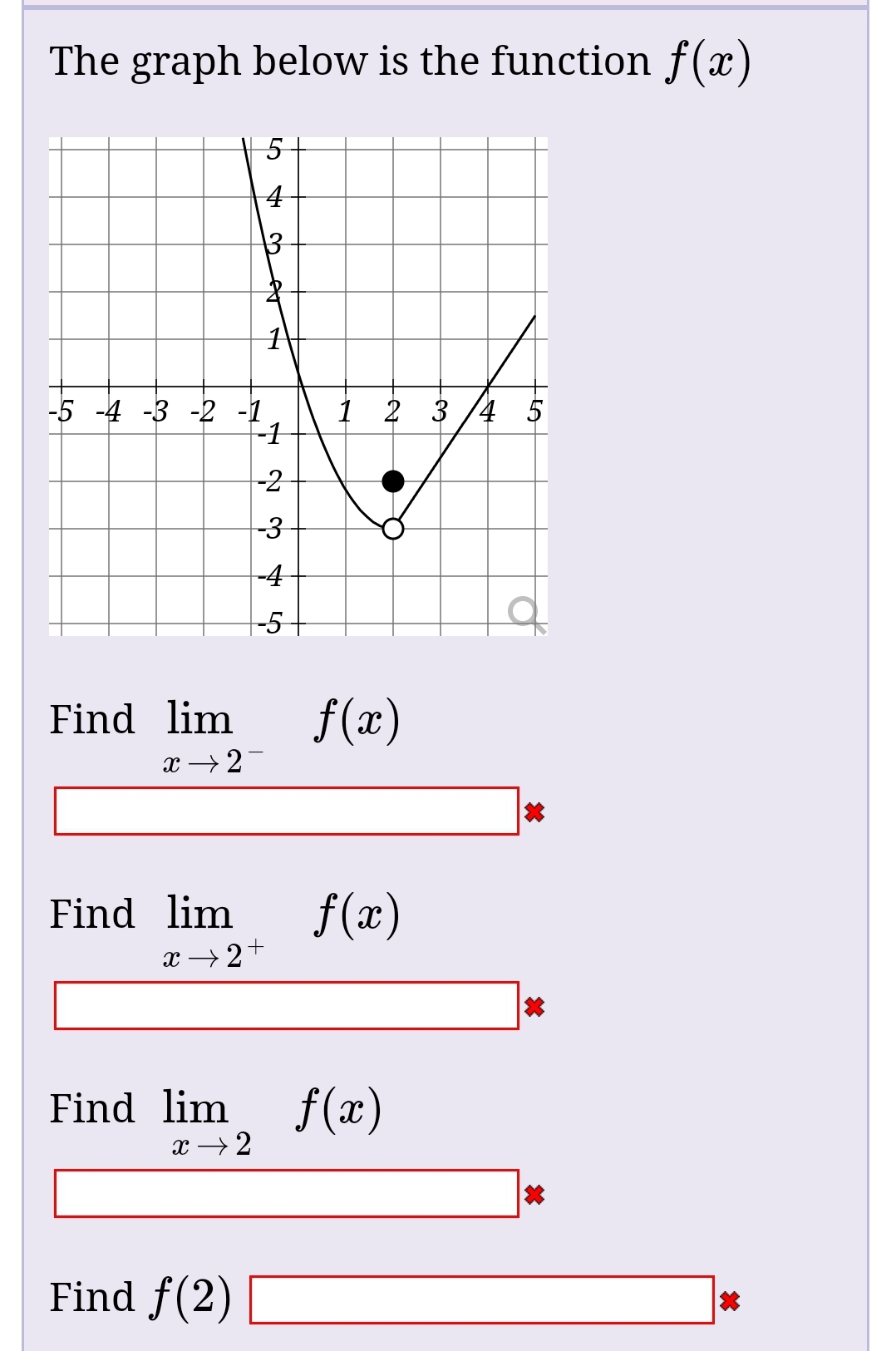
Answered The graph below is the function f(x) 5… bartleby
comparing graphs of f and it's first and second derivatives. Increasing/decreasing intervals, concavity, max/min

Ex 12.1, 27 Find lim x>5 f(x) where f(x) = x 5 Teachoo
Using the formulas from above, we can start with x=4: f (4) = 2×4+3 = 11 We can then use the inverse on the 11: f-1(11) = (11-3)/2 = 4 And we magically get 4 back again! We can write that in one line: f-1( f (4) ) = 4 "f inverse of f of 4 equals 4" So applying a function f and then its inverse f-1 gives us the original value back again: